Für ein besseres Verständnis wird dringend geraten, zuerst diesen Artikel hier durchzuarbeiten …
Motivation
Aus dem letzten Projekt waren noch zwei Fragestellungen übergeblieben:
- Könnte man nicht auch die kürzeren Fließkommaformate für neuronale Netze (typischerweise) nebst passender mathematischer Operation selbst implementieren?
- Wäre es dann möglich, entsprechende ‘custom’ Mnemonics (opcodes) im Compiler nachzurüsten? Und wenn ja: Wieviel Aufwand wäre hierfür zu treiben? Diesen Themen widmet sich dieses ‘Projekt’ …
1. Warum spielen die kurzen 16-Bit-Floats überhaupt so eine Rolle?
Der Platz auf einem Chip (oder - wie hier - dem FPGA) ist normalerweise begrenzt, d.h. ’teuer’. Umgekehrt kommt es bei Anwendungen im Graphikbereich (3d) oder auch neuronalen Netzen nicht so sehr auf die Genauigkeit an. Daher kann es sinnvoll sein, einen Datentyp zu verwenden, der praktisch den halben Platz einspart (50%!) und dafür schon in der ersten (dezimalen) Nachkommastelle nicht mehr so ganz exakt ist …
2. FP16, das(!) IEEE 754-2008 Format oder was?
Da ich im letzten Projekt bereits mit IEEE 754 Fließkommazahlen operiert hatte, schien es naheliegend, das dort beschriebene
16-bit Fließkommaformat (1 Bit Vorzeichen, 5 Bit Exponent, 10 Bit Mantisse) zu unterstützen.
Nachdem ich mich bereits eine Woche damit beschäftigt hatte (und die Zerlegung bzw.
Zusammensetzung sowie die einfache Addition schon am Laufen hatte), stieß ich auf einen Artikel (Link leider nicht gemerkt - shit happenz 🤔!),
der die im Laufe der Zeit entstandenen verschiedenen Formate miteinander verglich und ihre jeweiligen Stärken herausarbeitete.
Es leuchtete mir unmittelbar ein, daß allein die Konversion von 32-Bit-Float zu 16-Bit-Float (und zurück) einen Gutteil der
möglichen Performance-Gewinne bei FP16-Verwendung zunichte machen könnte.
Viel besser erschien da doch bfloat16 mit seinem einfachen Abschneiden der Mantisse,
d.h. im Wesentlichen wird halt nur das halbe (32-Bit-)Wort kopiert (bzw. umgekehrt der Rest mit Nullen aufgefüllt).
Also nochmal das Ganze von vorne mit ‘bfloat16’ …
Einer der ganz großen Vorteile war natürlich, daß es sich hier um denselben Aufbau handelt wie beim bereits im letzten Projekt
implementierten IEEE 754 32-Bit Floattyp, lediglich die Mantisse wird von 23 auf 7 Bit reduziert (also: 1 Bit Vorzeichen,
8 Bit Exponent, 7 Bit Mantisse).
Dies ermöglicht die 1:1 Wiederverwendung des existierenden Rechenwerks. Streng genommen bräuchten nur die fehlenden Mantissenbits
mit Nullen aufgefüllt werden, ich habe aber gleich die wenigen Adaptionen vorgenommen um ‘wirklich’ mit den kürzeren Formaten
zu rechnen.
3. Eine nützliche Operation
Der Speicherverbrauch für die Daten (On-Chip wohlgemerkt!) ist jetzt reduziert, was also damit anfangen?
Vor ein paar Jahren habe ich mich ein wenig für die Technik hinter den neuronalen Netzen interessiert (wer nicht?), und zu diesem
Zweck ’toten Baum’ studiert (Tariq Rashid, ‘Neuronale Netze selbst programmieren’, O’Reilly, ISBN 978-3-96009-043-4).
Das dortige größte (Python-)Beispielprogramm hatte ich für mich leicht abgewandelt und mit einer Qt5 Oberfläche versehen (es handelt
sich um die Auswertung für den ‘Standard’-MNIST Datensatz für die Handschrifterkennung von
Zahlen auf Überweisungsträgern).
Bei Durchsicht der ‘alten’ Quellen stieß ich auf folgende zentrale Bestimmungsfunktion für den laufenden Betrieb (das Modell
liegt hier bereits vor - es ist zeitunkritisch und kann vorab berechnet werden - und wird hier auch direkt von der Platte geladen …):
Auszug:
def query(self,inputs_list):
'''Query the neural network'''
# Convert inputs list to 2nd arrays
inputs = numpy.array(inputs_list,ndmin=2).T # Transpose ...
# Calculate signals into hidden layer
hidden_inputs = numpy.dot(self.wih,inputs) # Dot/inner matrice product
# Calculate the signals emerging from hidden layer
hidden_outputs = self.activation_function(hidden_inputs)
# Calculate signals into final output layer
final_inputs = numpy.dot(self.who,hidden_outputs)
# Calculate the signals emerging from final output layer
final_outputs = self.activation_function(final_inputs)
return final_outputs
Zentral ist hier die Funktion numpy.dot(), diese berechnet das innere (‘dot’) Produkt von Matrix & Vektor (bzw. Zeilenvektor & Spaltenvektor). Würde man diese Operation auf das FPGA verlagern, sollte sich die Performance doch verbessern lassen? Wir ignorieren hier mal die Problematik des Python-zu-C-Marshalling etc. …
Es zeigt sich, das im vorliegenden Fall die Daten als 28x28 Punktmatrix vorliegen (der ursprünglichen ‘Scan’-Auflösung), womit sich
eine Eintragslänge von 784 Werten ergibt. Im Programm wird effektiv jeweils mit einem ‘hidden layer’ von 200 Knoten gerechnet woraus
bei dem schlichten numpy.dot() bereits mit einer Matrix mit 200 Zeilen à 784 Spalten gerechnet wird. Oophs, das wird wohl kaum auf den
Chip passen!
Also eine Nummer kleiner: Jede Zeile einzeln berechnen - ergibt auch jeweils nur einen Ergebniswert (den ‘Skalar’).
Wir brauchen also eine Operation, die einen Zeilenvektor mit 784 Werten mit einem Spaltenvektor von 784 Werten Länge multipliziert.
So etwas kann für (z.Bsp.) eine RISC-V CPU in geradezu idealer Weise zerlegt werden in ‘fused’ multiply/add Befehle. Außerdem können mehrere Rechenkerne das Problem sehr gut parallel ermitteln, d.h. die Zeiten lassen sich fast gemäß Kernzahl herunterdrücken, lediglich am Ende müssen die Einzelsummen noch separat addiert werden (leider werden bei mir effektiv nur zwei 16-Bit-Rechenwerke auf’s FPGA passen …).
4. Implementierung
Hier wird parallel zur mitgelieferten vexriscv-CPU ein Verarbeitungs(Master-)knoten mit zwei Rechenwerken installiert.
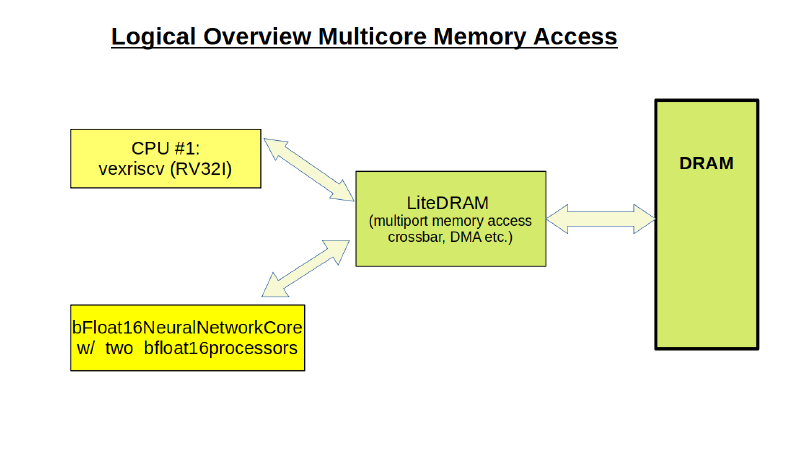
Das Projekt liegt auf unserem Git-Server. Es kann einzeln übersetzt werden, ist jedoch eigentlich als Erweiterung für das Risq5-Projekt gedacht. Es enthält nur eine Operation (dot product) sollte jedoch als Beispiel verstanden werden für die Implementierung weiterer nützlicher Funktionen.
5. Ergebnisse
Im vorliegenden Vergleichsfall mit einem Testprogramm in C ergibt sich eine Performance-Verbesserung (bei 2 Kernen) um den Faktor 7-10. Der langsamste Teil (und der Teil mit etwas Jitter) ist der DRAM-DMA-Transfer zum FPGA. Auf einem größeren FPGA mit mehr Kernen ließe sich natürlich noch erheblich mehr herausholen …
6. Das ‘Sahnehäubchen’ - RISC-V Opcode-Support im gcc
Ideal wäre eine Instruktion wie z.B.: matmul <rd>,<rs1>,<rs2> (ok, eigentlich wäre ‘vecmul’ oder ‘dotprod’ korrekter gewesen 🤔 …) wobei
- <rs1> das Register mit der Basisadresse der Matrixzeile (des Zeilenvektors) im RAM bezeichnet,
- <rs2> die Basisadresse des Spaltenvektors im RAM ist und
- in <rd> wird der (skalare) Ergebniswert zurückgemeldet.
Diese Instruktion könnte dann per Inline-Assembly in jedem C Programm Verwendung finden …
Eigentlich gäbe es wohl bereits passende Instruktionen in der RISC-V Vector-Extension, da diese aber niemals auf das hier verwendete kleine Lattice-FPGA passen würden (& das echt viele Instruktionen sind!), habe ich einfach die M-Extension erweitert (komplett Non-standard! Eigentlich Integer! Grauslig 💀 …).
Die ursprüngliche Annahme war ‘LLVM ist modularer (moderner) aufgebaut als der gcc’. Nachdem ich mich fast zwei Wochen mit LLVM - ohne so recht voranzukommen - herumgeschlagen hatte (ich wollte gleich eine neue Architektur einführen um dann das Backend zu erweitern …), habe ich es lieber mit dem gcc versucht.
Außerdem 💡: AUS was würde eigentlich in diese Instruktion übersetzt, also welche IL-Instruktion(en) käme(n) da wohl in Frage? Vermutlich gäbe es gar nichts Passendes 🗑 (es finden sich wohl bisher nur Proposals ), d.h. es würde eh’ nur Inline-Assembly zur Nutzung in Frage kommen.
Also gcc (für riscv):
git clone https://github.com/riscv/riscv-gnu-toolchain
cd riscv-gnu-toolchain
git submodule update --init --recursive
mkdir build
cd build
../configure --prefix=/<your_path>/riscv-gnu-toolchain/pub --enable-multilib
make report-linux SIM=qemu
Was soll ich sagen? In zwei Dateien für die RISC-V Opcodes zusätzliche Makros für die neue Mnemonic eintragen (für Assembly & Disassembly), Toolchain neu übersetzen und … läuft 👍!
Wie findet man die richtigen Dateien? Ich habe mir die ‘mulhu’ Instruktion herausgesucht zum grep’en da sie hinreichend ’exotisch’ ist (klingt auch irgendwie nach H.P.Lovecraft 🎃):
grep -r "mulhu" .
Im Ergebnis findet sich neben unwichtigen Binärdateien (und einigem ‘Gemüse’ im ignorierbaren ’testsuite’ Unterordner bzw. bei anderen Prozessor-Architekturen & dem Simulator qemu) die Datei riscv-opc.h, allerdings in zwei Pfaden innerhalb des ‘riscv-gnu-toolchain’ Projekts (beide Dateien sind gleich aufgebaut) - unter .riscv-gdb/include/opcode & ./riscv-binutils/include/opcode. Hier trägt man an zwei Stellen die neuen Daten ein:
...
#define MATCH_FENCE_TSO 0x8330000f
#define MASK_FENCE_TSO 0xfff0707f
// MATMUL instruction (MUL w/ one bit higher!)
#define MATCH_MATMUL 0x06000033
#define MASK_MATMUL 0xfe00707f
// MATMUL end
#define MATCH_MUL 0x2000033
#define MASK_MUL 0xfe00707f
#define MATCH_MULH 0x2001033
#define MASK_MULH 0xfe00707f
...
...
DECLARE_INSN(fence_i, MATCH_FENCE_I, MASK_FENCE_I)
// matmul instruction added
DECLARE_INSN(matmul, MATCH_MATMUL, MASK_MATMUL)
// matmul end
DECLARE_INSN(mul, MATCH_MUL, MASK_MUL)
DECLARE_INSN(mulh, MATCH_MULH, MASK_MULH)
...
MATCH_<str> ist die Basiscodierung, MASK_<str> ist der Filter um die Basiscodierung zu extrahieren.
Hinweis: Ich hatte zunächst ./org-riscv-binutils/include/opcode/riscv-opc.h übersehen, sie scheint aber im vorliegenden Fall nicht relevant zu sein …
Woher weiss man, wie ein neue Opcode-Kodierung aussehen darf?
Die Bits 0 bis 6 enthalten die Instruktionstypkennung, 0x33 ist eine ‘R-Type’ Instruktion (‘register (only)’).
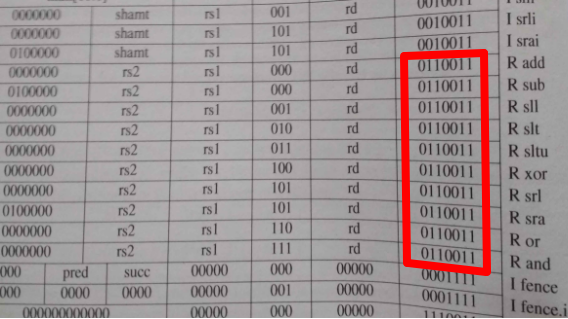
Die M-Extension ist hier in den Bits 26 bis 31 kodiert (als 0000001b, im Basissatz ‘I’ sind noch 0000000b
und 0100000 belegt).
Dazu hier mal die originale M-Extension (Integer Multiply/Divide) Kodierungstabelle:
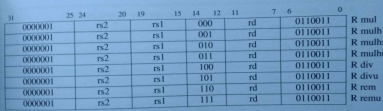
In den Bits 26 bis 31 könnte man also noch jede Menge neue Funktionen einführen. Ich habe im vorliegenden Fall lediglich das Bit 26 zusätzlich zum Bit 25 gesetzt …
Nach erfolgreicher Neuübersetzung der Toolchain (make clean, dann make) kann man jetzt Folgendes kompilieren (test.c):
#pragma GCC diagnostic ignored "-Wunused-function"
static void testmatmul(void)
{
__asm__ __volatile__ ("\
matmul x0,x0,x0 # 'Pure' opcode (all regs=0) \n\
matmul t2,t0,t1 # t0=Adress of (matrice) row, t1=column vector, t2=(scalar)result \n\
");
}
<my_local_path>/riscv64-unknown-elf-gcc -march=rv32im -mabi=ilp32 -S test.c
für den Assembly-Output, ansonsten reicht
<my_local_path>/riscv64-unknown-elf-gcc -march=rv32im -mabi=ilp32 test.c -o test
Hier der Auszug aus test.s:
...
.text
.align 2
.type testmatmul, @function
testmatmul:
addi sp,sp,-16
sw s0,12(sp)
addi s0,sp,16
#APP
# 6 "test.c" 1
matmul x0,x0,x0 # 'Pure' opcode (all regs=0)
matmul t2,t0,t1 # t0=Adress of (matrice) row, t1=column vector, t2=(scalar)result
# 0 "" 2
#NO_APP
nop
lw s0,12(sp)
addi sp,sp,16
jr ra
...
Das Ergebnis-Executable sollte wohl besser richtig disassembliert werden (zur Prüfung der Hex-Codierung):
<my_local_path>/riscv64-unknown-elf-objdump -D -m riscv test >test.dis
Hier der Auszug aus test.dis (schon hilfreicher!):
...
00010144 <testmatmul>:
10144: ff010113 addi sp,sp,-16
10148: 00812623 sw s0,12(sp)
1014c: 01010413 addi s0,sp,16
10150: 06000033 matmul zero,zero,zero
10154: 066283b3 matmul t2,t0,t1
10158: 00000013 nop
1015c: 00c12403 lw s0,12(sp)
10160: 01010113 addi sp,sp,16
10164: 00008067 ret
...
Hat geklappt 👍!
7. Was noch zu tun bleibt …
Leider paßt die ganze Logik gar nicht mit dem eigenen Risq5-Kern auf das kleine Lattice-FPGA. Das Ganze müsste also noch auf eine andere Zielplattform mit größerem FPGA verschoben werden. Außerdem müssen die 16-Bit-Rechenwerke noch mit der Logik des Risq5-Kerns verschmolzen werden, in etwa wie hier dargestellt:
aus libmodules/instruction_decode.py im Risq5-Projekt
...
If(regs.op == 0x33, # R-Type
If(regs.f3 == 0x00, # add/sub/mul
If(regs.f7 == 0x00, # add rd, rs1, rs2 (all indexes prep'd already!)
NextValue(regs.rd_wrport.dat_w, regs.xs1s + regs.xs2s),
).Elif(regs.f7 == 0x20, # sub rd, rs1, rs2
NextValue(regs.rd_wrport.dat_w, regs.xs1s - regs.xs2s),
).Elif(regs.f7 == 0x01, # mul rd, rs1, rs2 (M extension)
NextValue(regs.rd_wrport.dat_w, regs.rd_mul64s[0:32]),
).Elif(regs.f7 == 0x03, # matmul rd, rs1, rs2 (test!)
... hier Parameterübergabe etc. ...
),
...
The remaining plumbing work is left as an exercise to the reader … grrrh 💀 ☮ 🗣 (& sufficient FPGA resources assumed …)
Jedenfalls solange, bis ich an ein größeres FPGA (mit LAN-Zugang wg. des Risq5-Debuggers) komme.
Eine Verbesserung wäre auch das Ausfiltern, d.h. aus 32-Bit Float-Array direkt nur halbe Worte lokal im FPGA übernehmen (‘striding’), dann könnte ein Umkopieren komplett entfallen.
 Mastodon
Mastodon